图论-图解-克鲁斯卡尔 (Kruskal) 算法
在图论中,克鲁斯卡尔 (Kruskal) 算法是用于求解图的最小生成树的典型算法。本文试图用一种简单易懂的图解步骤方式来讲解该算法。
克鲁斯卡尔 (Kruskal) 算法
概念
设图 G=<V,E> 是一个具有 n 个顶点的带权连通无向图。图 T=<V, TE> 是图 G 的最小生成树。
- V 是图 T 的顶点集。
- TE 是图 T 的边集。
如何由图 G 生成图 T,这就是该算法要解决的问题。
算法
- 将图 G 中的边按照权重从小到大排序。
- 依次选取每条边,若选权的边未使图 T 形成回路,则加入到边集 TE 中; 否则舍弃,直到 TE 中包含 n - 1 条边为止。
示例图解
- 带权连通无向图 G
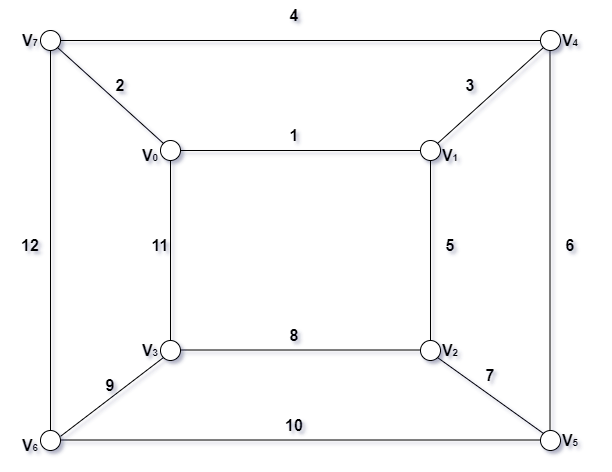
图解步骤
- 按权从小到大排序
| 边 | 权 |
|---|---|
| (V0,V1) | 1 |
| (V0,V7) | 2 |
| (V1,V4) | 3 |
| (V4,V7) | 4 |
| (V1,V2) | 5 |
| (V4,V5) | 6 |
| (V2,V5) | 7 |
| (V2,V3) | 8 |
| (V3,V6) | 9 |
| (V5,V6) | 10 |
| (V0,V3) | 11 |
| (V6,V7) | 12 |
- 取第一条边
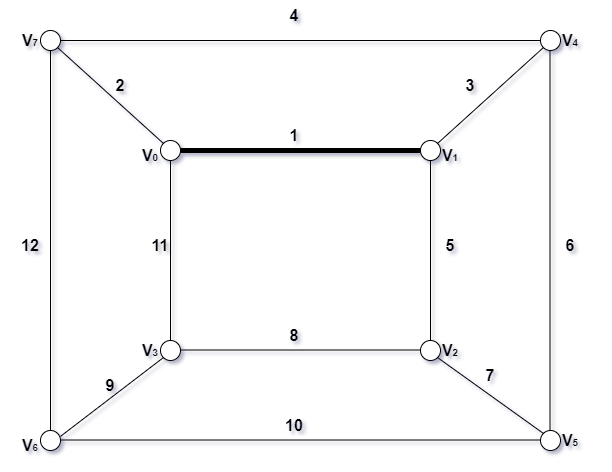
- 取第二条边
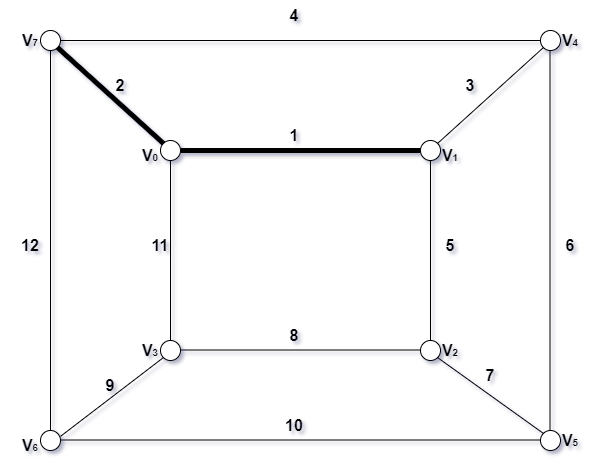
- 取第三条边
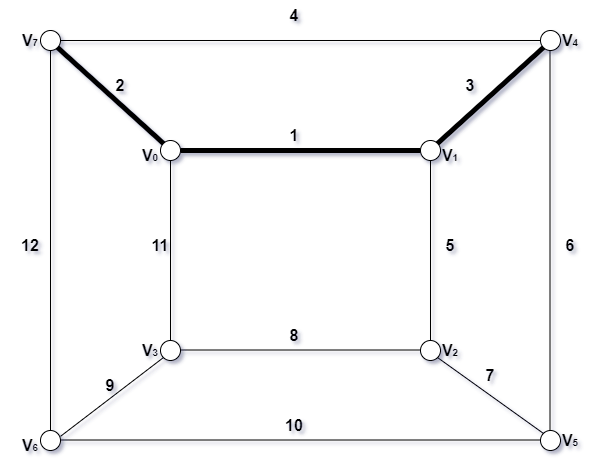
- 取第四条边,构成了回路,舍弃
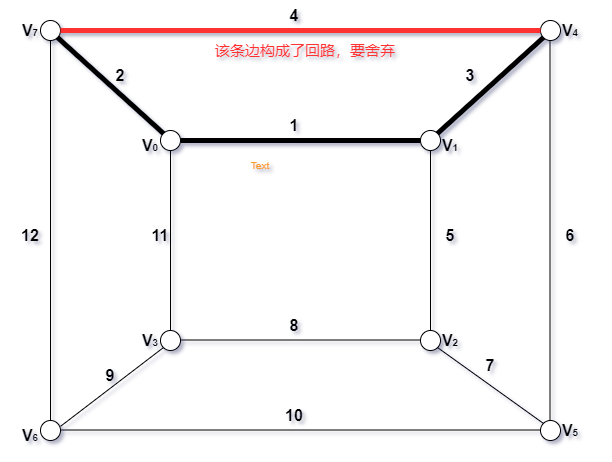
- 取第五条边
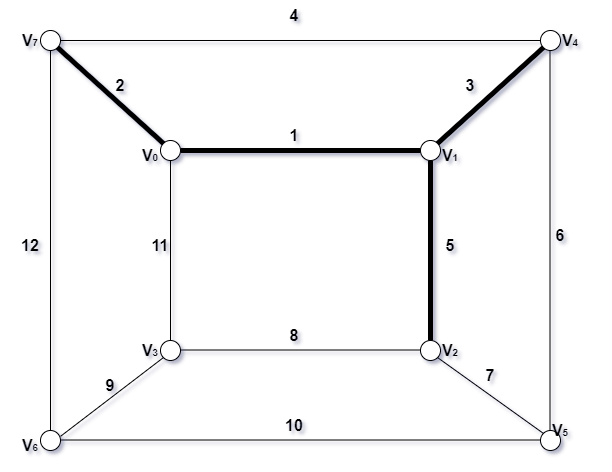
- 取第六条边
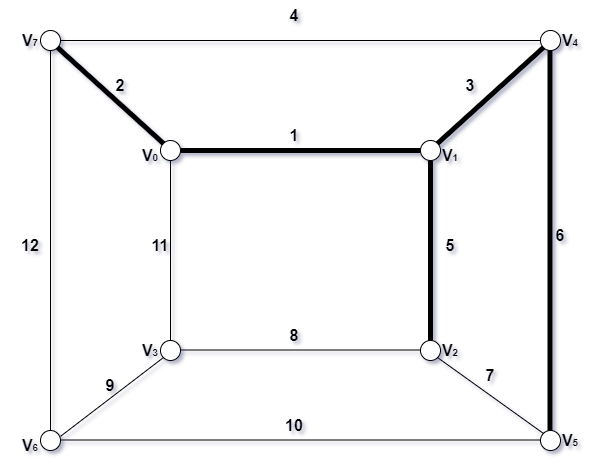
- 取第七条边,构成了回路,舍弃
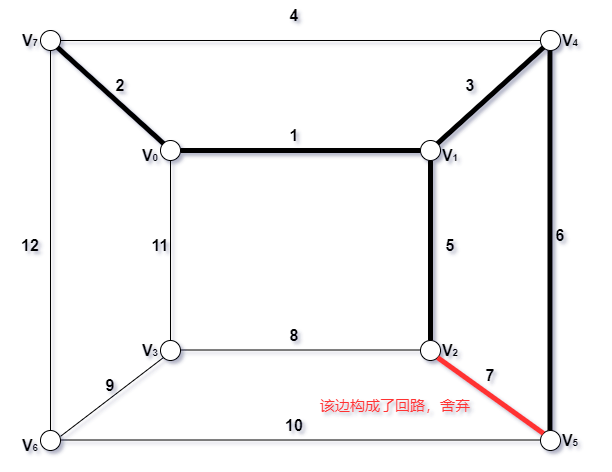
- 取第八条边

- 取第九条边
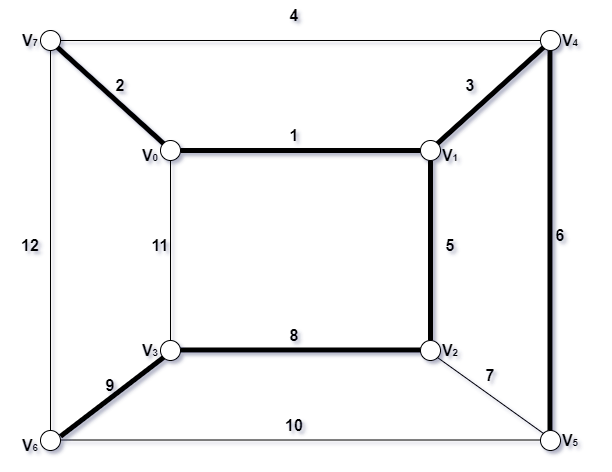
此时的边数 = n(节点个数) - 1 = 8 - 1 = 7 条了,结束。