机器学习入门-算法-协同过滤简介

本文是机器学习常用算法之协同过滤算法系列篇中的第一篇,主要讲解了协同过滤的基本概念,如何求相似度,以及如何根据基于物品的协同过滤对物品进行评分。
目录
什么是协同过滤(Collaborative Filtering)
维基百科: 协同过滤(collaborative filtering)是一种在推荐系统中广泛使用的技术。 该技术通过分析用户或者事物之间的相似性(“协同”),来预测用户可能感兴趣的内容并将此内容推荐给用户。
协同过滤实际上是一种数学方法,它通过将一个用户与所有其它用户进行比较,预测该用户给某一项目的评分。
例如:为了预测用户A对某一特定项目的评分,首先需要计算用户A和其它所有用户的相似度。取出与用户A最相似的用户, 然后计算出用户A与所有最相似用户对这一项目的预测评分。
协同过滤分类
基于用户的协同过滤
一般来说,通过用户的喜好特征找出与他相似的用户, 再将相似的用户对物品有相同行为(比如购买了该物品)推荐给目标客户。
如下图所示: 用户A喜欢物品1和物品3,用户C也喜欢物品1和物品3。所以我们推测用户A和用户C有很大的相似度(喜好可能相同)。 而A对物品4还没有相关行为,所以把用户C喜欢的物品4推荐给用户A。
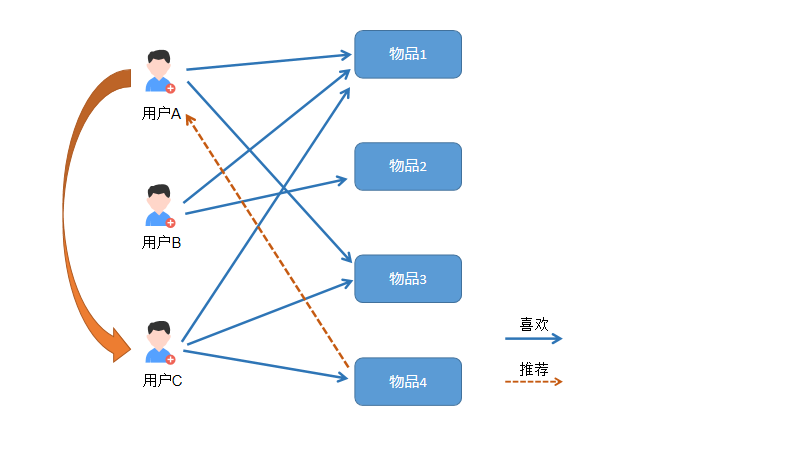
基于物品的协同过滤
一般来说,通过物品的特征X找出与它相似的物品, 再将相似的物品推荐给目标客户。
如下图所示: 用户A喜欢物品1和物品3,用户C也喜欢物品1和物品3。所以我们推测物品1和物品3有很大的相似度(特征可能相同)。 而用户B喜欢了物品1,而物品3和物品1相似,所以自动将物品3推荐给用户B。
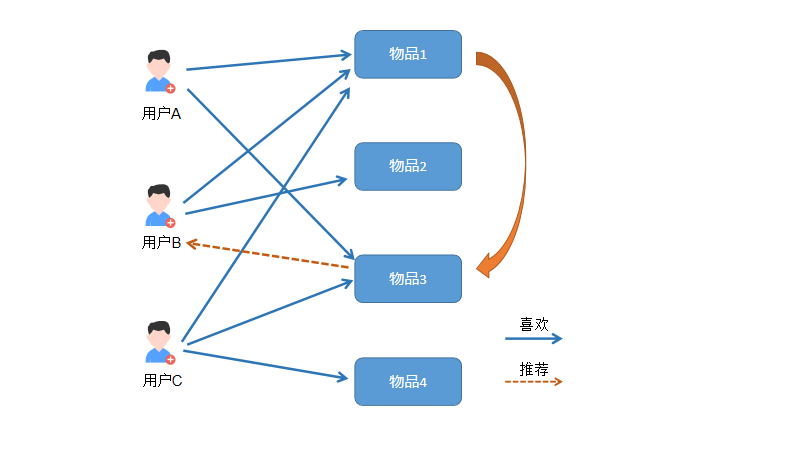
相似度
正如前面所讲,协同过滤不管是基于用户还是基于物品,首先都要找到相似物品或相似用户。那么如何求得用户或物品的相似度呢?本节将会做详细讲解。
书籍评分数据
我们以推荐书籍来举例,有如下书籍评分数据(分值1-5,分值越高表示越喜欢,分值越低表示不喜欢),分别用余弦相似度和Pearson(皮尔逊)相似度来计算用户相似度。
| 用户/书籍 | 精益创业 | 会计学 | 微积分 | 育儿 | 投资 | 时间管理 | 情绪控制 |
|---|---|---|---|---|---|---|---|
| 用户A | 4 | - | - | 5 | 1 | - | - |
| 用户B | 5 | 5 | 4 | - | - | - | - |
| 用户C | 1 | - | - | 1 | - | - | - |
| 用户D | - | 3 | - | - | - | - | 3 |
余弦相似度
余弦相似度,也叫做余弦距离,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。根据余弦定理可以得到两个向量夹角的cos值。
余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似,这就叫"余弦相似性"。
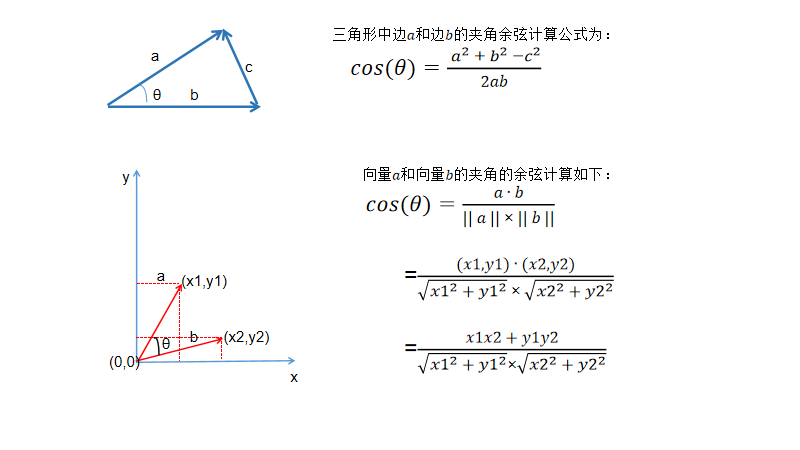
现在我们依次来求书籍评分数据的用户相似度。 根据公式,用户A、用户B的相似度即为 A,B 对书籍《精益创业》的评分之积 比上A,B对7本书的评分的模。
| 用户/书籍 | 精益创业 | 会计学 | 微积分 | 育儿 | 投资 | 时间管理 | 情绪控制 |
|---|---|---|---|---|---|---|---|
| 用户A | 4 | - | - | 5 | 1 | - | - |
| 用户B | 5 | 5 | 4 | - | - | - | - |
| 用户C | 1 | - | - | 1 | - | - | - |
| 用户D | - | 3 | - | - | - | - | 3 |
- 用户A,B相似度计算如下: $$ \color{red} sim(A,B) = \frac{ 4\times5 }{ { \sqrt{ 4\times4+5\times5+1\times1} } \times {\sqrt{5\times5+5\times5+4\times4}} } = 0.38 $$
- 用户A,C相似度计算如下: $$ \color{red} sim(A,C) = \frac{ 4\times1 + 5\times1 }{ { \sqrt{ 4\times4+5\times5+1\times1} } \times {\sqrt{1\times1+1\times1}} } = 0.98 $$
通过计算结果来看,sim(A,C) > sim(A,B) 。用户A,C的相似度 远大于 用户A,B的相似度。但通过观察上面的表格看出,用户A,B都喜欢《精益创业》这本书(评分在4分及5分),但是A,C没有共同喜欢的书籍(C评分为1分表示不喜欢)。 所以推断A,B比A,C相似度高才对。 但是计算结果却相反,这到底是什么原因?
从表格上看,这是因为用户对每一本书的打分在总打分的比重是不一样的。比如,用户A的总分是10分。 《精益创业》打分占比为4/10。用户B的总分为14分,《精益创业》占比为4/14。用户C的总分为2分,《精益创业》占比为1/2。
一般来说,上面的余弦相似度计算没有把缺失的维度值考虑进去(也就是没有把用户未评分项目考虑进来),进而给相似度计算带来了差异。
皮尔逊相似度
为了解决余弦相似度计算带来的相似度差异问题,我们采用皮尔逊算法。皮尔逊算法比余弦距离更加重视数据集的整体性。
该算法运用皮尔逊相关性思想计算向量余弦相似度,得到皮尔逊相关系数,它是余弦相似度在维度值缺失下的一种改进。
皮尔逊相关性
皮尔逊是一种相关性度量方法,主要依靠计算得出的皮尔逊相关系数度量。 皮尔逊相关系数输出范围为-1到+1,0代表无相关性,负值为负相关,正值为正相关。
几何上来讲,皮尔逊相关系数是余弦相似度在维度值缺失情况下的一种改进。 皮尔逊系数就是在使用cos计算两个向量(cos<a, b> = a • b / |a|•|b|)时进行中心化。
皮尔逊相关系数的一般思路是,对每个向量,先计算出所有元素的平均值,然后向量中每个维度的值减去这个平均值,得到的这个向量被称为 中心化的向量。这样的操作也叫做中心化。
注: 机器学习要计算向量余弦相似度的时候, 由于向量经常在某个维度上有数据的缺失, 预处理阶段都要对所有维度的数值进行中心化处理。
注: 皮尔逊相关系数相关分类
- 0.8-1.0 极强相关
- 0.6-0.8 强相关
- 0.4-0.6 中等程度相关
- 0.2-0.4 弱相关
- 0.0-0.2 极弱相关或无相关
求解步骤
- 步骤一:计算平均值
| 用户/书籍 | 精益创业 | 会计学 | 微积分 | 育儿 | 投资 | 时间管理 | 情绪控制 | Mean(平均值) |
|---|---|---|---|---|---|---|---|---|
| 用户A | 4 | - | - | 5 | 1 | - | - | 10/3 |
| 用户B | 5 | 5 | 4 | - | - | - | - | 14/3 |
| 用户C | 1 | - | - | 1 | - | - | - | 2/2 |
| 用户D | - | 3 | - | - | - | - | 3 | 6/2 |
- 步骤二: 减去平均值
| 用户/书籍 | 精益创业 | 会计学 | 微积分 | 育儿 | 投资 | 时间管理 | 情绪控制 |
|---|---|---|---|---|---|---|---|
| 用户A | 2/3 | - | - | 5/3 | -7/3 | - | - |
| 用户B | 1/3 | 1/3 | -2/3 | - | - | - | - |
| 用户C | 0 | - | - | 0 | - | - | - |
| 用户D | - | 0 | - | - | - | - | 0 |
- 步骤三: 计算余弦相似度
| 用户/书籍 | 精益创业 | 会计学 | 微积分 | 育儿 | 投资 | 时间管理 | 情绪控制 |
|---|---|---|---|---|---|---|---|
| 用户A | 2/3 | - | - | 5/3 | -7/3 | - | - |
| 用户B | 1/3 | 1/3 | -2/3 | - | - | - | - |
| 用户C | 0 | - | - | 0 | - | - | - |
| 用户D | - | 0 | - | - | - | - | 0 |
用户A,B的相似度 $$ \color{red} sim(A,B) = \frac{ \frac2 3\times\frac1 3 }{ { \sqrt{ (\frac 2 3\times\frac 2 3) + (\frac5 3\times\frac 5 3) + (-\frac7 3\times-\frac7 3)} } \times {\sqrt{(\frac1 3\times\frac1 3)+(\frac1 3\times\frac1 3)+(-\frac2 3\times-\frac2 3)}} } = 0.09 $$
用户A,C的相似度
用户C的评分都为0,显然A,C的相似度是0。 sim(A,C) = 0
由此可见,这次的计算结果与之前的推断是相符的。用户A,B的相似度比A,C的相似度高。
协同过滤预测打分
接下来,我们分别以物品和用户的维度来对物品或用户进行评分预测。
物品协同过滤
以下是用户A-G对三本书的评分数据。 我们怎么推断用户D对《精益创业》这本书的喜欢程度呢?即评分是多少?
| - | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 精益创业 | 1 | - | 3 | ? | - | 5 | - |
| 会计学 | - | - | 5 | 4 | - | - | 4 |
| 微积分 | 2 | 4 | - | 1 | 2 | - | 3 |
步骤一: 求平均值
| - | A | B | C | D | E | F | G | mean |
|---|---|---|---|---|---|---|---|---|
| 精益创业 | 1 | - | 4 | ? | - | 5 | - | 10/3 |
| 会计学 | - | - | 5 | 4 | - | - | 4 | 13/3 |
| 微积分 | 2 | 4 | - | 1 | 2 | - | 3 | 9/4 |
步骤二: 减去平均值
| - | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 精益创业 | -7/3 | - | 2/3 | ? | - | 5/3 | - |
| 会计学 | - | - | 2/3 | -1/3 | - | - | -1/3 |
| 微积分 | -1/4 | -1/4 | - | -1/4 | -1/4 | - | 1 |
- 步骤三: 分别计算物品《精益创业》(含自己)和其它所有物品的相似度
| - | A | B | C | D | E | F | G | 相似度 |
|---|---|---|---|---|---|---|---|---|
| 精益创业 | -7/3 | - | 2/3 | ? | - | 5/3 | - | 1.0 |
| 会计学 | - | - | 2/3 | -1/3 | - | - | -1/3 | 0.046 |
| 微积分 | -1/4 | -1/4 | - | -1/4 | -1/4 | - | 1 | 0.048 |
$$ \color{red}sim(精益创业,精益创业)=1 $$ $$ \color{red}sim(精益创业,会计学)= \frac{ \frac2 3\times\frac2 3 } { { \sqrt{ (-\frac 7 3\times-\frac 7 3) + (\frac2 3\times\frac2 3) + (\frac5 3\times\frac5 3)} } \times {\sqrt{(\frac2 3\times\frac2 3)+(-\frac1 3\times-\frac1 3)+(-\frac1 3\times-\frac1 3)}} } = 0.046 $$ $$ \color{red}sim(精益创业,微积分)= \frac{-\frac7 3\times-\frac1 4 } { { \sqrt{ (-\frac 7 3\times-\frac 7 3) + (\frac2 3\times\frac2 3) + (\frac5 3\times\frac5 3)} } \times {\sqrt{(-\frac1 4\times-\frac1 4)+(-\frac1 4\times-\frac1 4)+(-\frac1 4\times-\frac1 4)+(-\frac1 4\times-\frac1 4)+(1\times1)}} } = 0.048 $$
- 步骤四: 根据以下公式计算评分
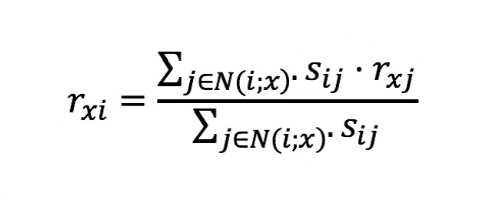
| - | A | B | C | D | E | F | G | 评分 |
|---|---|---|---|---|---|---|---|---|
| 精益创业 | 1 | - | 3 | 1.65 | - | 5 | - | 1.0 |
| 会计学 | - | - | 5 | 4 | - | - | 4 | 0.046 |
| 微积分 | 2 | 4 | - | 1 | 2 | - | 3 | 0.048 |
$$ \color{red}R14=\frac{(0.046\times4+0.048\times1)} {(0.046+0.048)}=1.65 $$
用户协同过滤
用户协同过滤和物品协同过滤原理是一样的,唯一的区别是计算时切换一下维度即可,这里就不在重复了。
物品和用户协同过滤对比
- 基于物品和基于用户的原理是相同的。
- 基于物品很少的数据就可以预测,但是基于用户需要大量数据。
- 一般来讲,基于物品比基于用户更具有实践性,在实际的推荐系统中用得更多。
参考资料
- 《推荐系统实践》项亮 著
- https://zh.wikipedia.org/wiki/%E5%8D%94%E5%90%8C%E9%81%8E%E6%BF%BE
- https://www.youtube.com/watch?v=h9gpufJFF-0
- https://developers.google.com/machine-learning/recommendation/collaborative/matrix
- https://zhuanlan.zhihu.com/p/95350982
- http://www.linkedkeeper.com/detail/blog.action?bid=1060
- https://medium.com/@sam.mail2me/recommendation-systems-collaborative-filtering-just-with-numpy-and-pandas-a-z-fa9868a95da2
(全文完)